你可知道新加坡的数学教育也很牛？-新东方前途出国

2016年11月，TIMSS2015的结果公布，新加坡学生位列榜首。同年12月6 日， OECD 也公布了PISA2015的测试结果，新加坡学生在数学、科学、阅读三个领域的排名又都排在了第一。 

　　其实，在TIMSS 和PISA 这两个著名的国际学生学业水平评估项目中，新加坡一直表现上佳。持续的高表现引发了各国观察、研究、思考新加坡基础教育的热情。 

　　新加坡的数学教育对我们的数学教育，有哪些可借鉴之处？ 

　　今天，我们以新加坡数学教育为切入点，数学教育作为新加坡教育的一张名片，其最大的目标不是让学生“刷题”，而是将问题解决置于核心地位。 

　　为了让大家直观感受新加坡的数学教育，先上一道数学题！

　　请听题，

　　谢丽尔的生日是下列日期中的一个？

　　5 月15 日，5 月16 日，5 月19 日，

　　6 月17 日，6 月18 日，

　　7 月14 日，7 月16 日，

　　8 月14 日，8 月15 日，8 月17 日。

　　谢丽尔把月份告诉了阿尔伯特，把日期告诉了伯纳德。

　　阿尔伯特说：“我不知道谢丽尔的生日，但我知道伯纳德也不知道。”

　　伯纳德说：“本来我不知道谢丽尔生日的，但听完阿尔伯特的话，我就确定了。”

　　阿尔伯特接着说：“那么，现在我也确定谢丽尔的生日了。”

　　谢丽尔的生日是哪一天？

　　你的脑子转过弯来了吗？

　　这道初中数学题曾在社交媒体上病毒式传播，“难倒了众生”。

　　这道新加坡用来测试14~15 岁中学生数学逻辑思维的题是为学业水平较高的学生准备的，但之所以出这种题型，并非出题的新加坡南洋理工大学喜欢标新立异，而是因为这道题契合了新加坡数学教育的理念：注重对数学概念的深层次理解，以便达到建立于理解之上的掌握乃至精通。而这正是新加坡数学教育方式为各国教育者熟知的一个显著特点，也是新加坡数学教材走向世界的“卖点”。 

　　▲新加坡数学课程“出口”多个国家 

　　秘诀之一：

　　“看上去很好理解”

　　上世纪八十年代，新加坡开启了从识记型教育向深层次理解型教育的大转型，新加坡教育部的课程设计专家们借鉴美国著名认知心理学家和教育家杰罗姆? 布鲁纳的相关理论，开发出了数学教学的三步法。布鲁纳将学习的过程分为三个步骤：运用实物—使用图画—运用符号，这就是新加坡数学三步法“实物—图画—抽象”三步法的理论渊源。 

　　在三步法的框架下，新加坡的学生，尤其是小学生，每堂数学课都是从积木、骰子、纸牌、硬币等实物开始的，这很容易理解，类似于我们教幼龄儿童数手指。

　　第二步是图画（pictorial），但不是山水花鸟，而是条状图。这是一种简单的数学建模，学生画出一个长条代表一个确定的数量，再按照比例画出与之相比较的数量，是大还是小，大多少、小多少，立刻一目了然了。

　　第三步才是抽象的列算式演算。

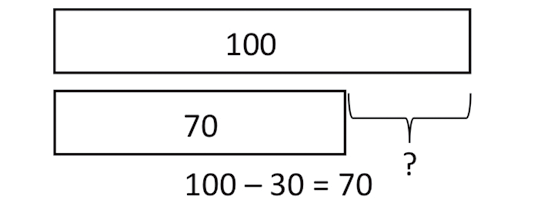
▲减法的条状图模型 

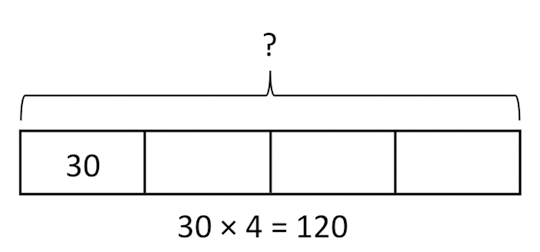
▲乘法的条状图模型 

　　条状图建模让学生得以直观地观察到数量之间的关系，也能在解答问题时“看到”抽象的概念，因此，会“看起来很好懂”。这比传统的数学教学多出了前两个步骤，力图让低龄的学生通过具象、可感的方式掌握数学方法，理解数学概念，被多国教育研究专家视为新加坡学生能够在PISA、TIMSS 上表现强劲的决胜法宝。 

　　在设计数学应用题时，课程专家们也会首先考虑和学生的生活密切相关的场景，这样有利于下一这位学生根据熟悉的情境快速建立起条状图模式，开始解题。 

　　秘诀之二：

　　“做起来很好理解”

　　到了中学阶段，知识的理解，以及基于理解的应用就很大程度上依靠学生的自主学习能力了，这个阶段，以学生为中心的教学法就派上了用场。 

　　在著名的莱佛士女子中学，数学教师的授课方式就是典型的学生中心型。以三角函数部分为例，当讲到“sin（x）+cos（x）= ？”时，老师会让学生把sin（x）的正弦图和cos（x）的余弦图上的点一个一个地叠加起来，绘出一幅新的图。这样，学生就发现：叠加起来之后，真的是一幅新的三角函数的图，而不是其他无规律的图。有些老师甚至会鼓励学生自行推导出微积分的公式来。

　　而当学到的知识能够用到生活当中时，理解的深度就更拓展了。数学建模就是其中的一个例子。 

　　比方说，三角函数中的图形转变，内容很艰深，单靠授课会很枯燥，教师就给学生布置相关的专题作业，比方说研究某地的气温变化状况，并尝试用一个三角函数来建模，最后预测该地此后一段时间的气温。如此把抽象的数学置于学生熟悉的某个环境中去，可以让他们清晰地看到数学作为一门精确的科学，是如何简化复杂问题的，也能体会到学以致用的乐趣。 

　　有时候，学生甚至欣喜地发现：自己“发明”了一个数学定理，因为它不是教师在课堂上逐步逐步传授的，而是自己利用线索、分析研究得出来的。有的数学老师甚至会邀请学校其他学科的老师一起来建有趣的“模”，如物理、化学、生物、数学老师大联手，将一个厕所伪造成犯罪现场，邀请学生来做侦探，进行调查研究。 

　　秘诀之三：

　　很有趣，也很实用

　　这下，我们就能理解，文章开头那道“难倒众生”的题目是如何进入新加坡初中生的试卷中的。因为数学概念和定理就是这样被猜测、理解和“发现”的。 

　　答案在此↓↓↓ 

　　除了数学逻辑思维，“谢丽尔的生日”还可作为统计学上“成比例错误减少”概念的生动显现。

　　谢丽尔的生日由两个变量组成：月份和日期，在缺乏任何补充条件的情况下，可能的生日有10 个，如果随机猜测的话，猜对的可能性只有10%，猜错的可能性高达90%。如何逐步减少猜错的概率，直至零呢？这就需要借助月份和日期之间存在的强相关性（比如，日期是18 日的话，月份只能是6 月，关联性高达100%）以及题干陈述中给出的条件成组或逐个排除选项。

　　首先，阿尔伯特说：“……但我知道伯纳德也不知道。”说明日期不是18 日、19 日（它们分别和相应的月份100% 相关），阿尔伯特只有在听到的月份不是5 月或6 月时，才可以肯定伯纳德不可能获知18 日或19 日，于是将可选项缩减为5 个，猜错的概率下降为80%。

　　紧接着，从阿尔伯特的陈述中，伯纳德推测出，阿尔伯特获知的是7 月或8 月，由此确定谢丽尔的生日，说明他获知的日期不是14 日，否则他仍然确定不了，进一步将选项缩减到7 月16 日、8 月15 日、8 月17 日，猜错概率进一步降为66%。

　　决定性的一步在于阿尔伯特的陈述：“哦，现在我也确定谢丽尔的生日了。”根据伯纳德的话，阿尔伯特推测他听到的日期是15 日、16 日、17 日中的一个，但如果他获知的是8 月，还是不能确定谢丽尔的生日，所以只能是7 月，7 月只有一个选项存在，猜错概率下降为零。

　　“谢丽尔的生日”在锻炼逻辑思维的同时，吸引着学生一步一步探索、认识，并深刻理解了“成比例错误减少”的概念，可以说是新加坡数学教育的一个有趣的折射。 

　　新加坡数学课程：

　　以数学问题解决为核心

　　在新加坡，学校的数学课程是由教育中心设置的。中小学所有年级都实施相同的课程，课程明确了每个年级的内容覆盖范围和评估标准。自20 世纪80 年代末期起，新加坡的数学课程就以“元框架”为构思核心，课程的规划和修订都是以其为基准的。 

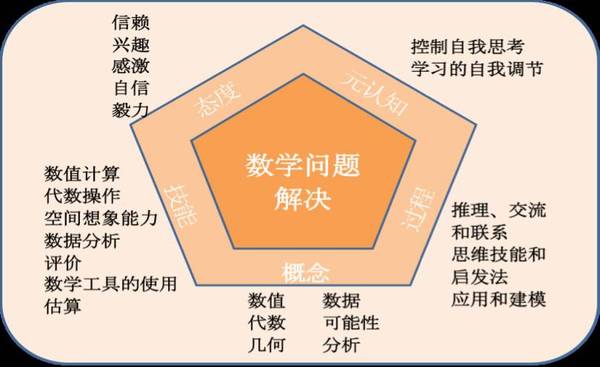
　　从这个课程框架图中可以看出，新加坡数学课程的总目标将数学问题解决置于数学学习的核心地位。 

　　比如，2013 年，新加坡一所街区小学的一组教师根据大纲中数学教学的原则，设计了一个现实问题解决的任务——餐馆问题。 

　　餐馆问题设置了一个情境：学生在一次聚餐中要花费大约30美元的钱。学生们需要从14 个菜品中选择消费，前提是能保证小组中的每个人都有一杯饮料并可以选择甜品。而这些菜的价格是这样设置的：1 篮炸鸡翅12 个共18 美元、1 杯橙汁2.5 美元、3 支冰淇淋4.5 美元，等等。这个任务涉及到数字的加减乘除等知识点，但其考验的最核心部分是学生的规划组合能力。

　　而在接触到真正的问题之前，作为过渡，教师向学生展示了与这个问题原理相似但是在情境上经过优化的问题，即前置任务。前置任务是书店问题，要求学生在学校的书店中花费整整2 美元。学生需要从9 种文具中选择消费，比如，有铅笔、橡皮、钢笔和尺子等文具，它们的价格分别为10 美分、20 美分、30 美分、50 美分，等等。

　　与之相对应的，针对这种转变，新加坡教育部也在教学方法指导上作了变革。 

　　在数学课程中，问题解决的启发法是作为教学过程的一部分被写入大纲的。 

　　小学水平的教学大纲中列出了11 种问题解决启发法，包括“表演出来”“使用图表/ 模型”和“解决问题的一部分”等；中学水平的教学大纲列出了13 种启发法，其中有2 种是小学大纲中没有的，即“使用方程”和“思考相关的问题”。 

　　近年来，许多新加坡学者一直致力于基于真实情境的问题解决的课堂教学改革，学生在数学学习中也越来越多地接触到完整的开放式任务。比如，在中学数学中，以综合的开放式任务作为评价策略的实验；在小学六年级数学中，使用完整的开放式数学任务的经验和困难的调查。 

　　有研究表明，通过使用“脚手架”和有意义的解释，学生们能积极地参与高层次的认知思考，而需要联系前后文的开放式数学任务正是这样的存在，其真实性为学生提供了在讨论中提升个人价值和自信的机会。 

　　此外，让学生接触这种开放式数学任务能让学生体会到真实世界的复杂性。在问题解决的过程中，学生们能将数学学习与真实世界联系起来。 

留学咨询请拨打 020-23336566         

　　更多留学资讯，关注广州新东方前途出国 https://liuxue.xdf.cn/guangzhou/        

地址：广州市天河区珠江新城珠江东路6号广州周大福金融中心34层        

官方微博：@广州新东方前途出国